【レビュー】5分で論理的思考力ドリル ちょっとむずかしめ編

以前購入した、ソニー・グローバルエデュケーション著の「5分で論理的思考力ドリル」シリーズ3作品のうち、すこーしだけむずかしくなっている「ちょっとむずかしめ編」についてレビューしたいと思います。

【レビュー】5分で論理的思考力ドリルレビュー

本書の特徴

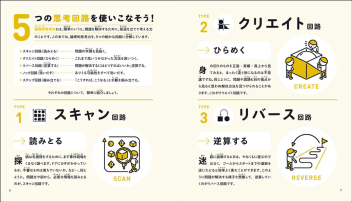
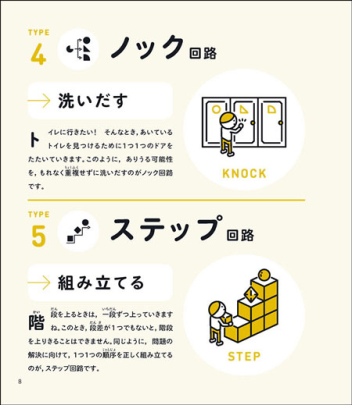
ソニーグローバルエデュケーションでは、論理的思考力を以下の５つの思考回路に分けて定義し、それらを総合的に成長させることによって、論理的能力の向上目指すように本書は作られています。

そもそもの「論理的思考力」とは簡単に言うと、
『ある問題をクリアするために、何を、どのように、どんな順番でといったことを考え・解決する能力』であると考えています。

それらを上記の「５つの思考回路」に合わせると以下のようになります。
１．スキャン回路で、「どんな問題が起きているのか」を整理。
２．クリエイト回路で、「問題に対する解決策（ゴール）」をひらめく。
３．リバース回路で、「解決策に至るまでのプロセス（スタート→ゴール）」を逆算する。
４．ノック回路で、「各プロセスの内容」を考え、抜け漏れがないか確認。
５．ステップ回路で、「各プロセスの順序」を整理し、１つ１つ組み立てる。

5分で論理的思考力ドリル　ちょっとむずかしめ編

5分で論理的思考力ドリルの「無印（標準）編」は銀色の表紙のものになっています。

5分で論理的思考力ドリルシリーズの全3種類のうち、この「ちょっとむずかしめ編」は、本シリーズ最後のドリルなだけあって、前作よりすこしだけ難しい問題が多くなっています。
最初の方ででつまづくかもしれませんが、出来なかったら次の問題をやるといった形で切り替えて行ってもいいかもしれません。
なぜか学研公式サイトでは、小学校１～６年生向けとの記載がありましたが、小学校高学年でないと自力では解けないと思います。

基本的な解き方としては、まずは5分間自力で考える。
それで分からなかったら、次のページにヒントが書いてあるので、それを読んでもう一度考える。（こっちも5分位）
それでも分からない場合は、答えを見て内容を理解する。といった形でうちでは進めています。
大事なのは、解けなかったとしても、答えを見て「あぁ・・なるほど！」と、答えを導き出すための過程（プロセス）と結果（答え＝ゴール）がしっかりと理解できれば万事OKかと思っています。

教材の内容

教材の内容を一部紹介しようと思います。

問題：ナンモンのテスト？
メグミは１問５点の問題と１問８点の問題でできた１００点満点のテストを受けました。
テストの結果は６２点でした。

テストの問題は全部で何問ありましたか？

といった問題になります。
標準編の例題であった、グーチョキパーの問題と似たような問題ですね。

まずは5分間自分で考えましょう！

それでも解けなければ以下ヒントを見てみましょう。

ヒント２番にあるように、最初にメグミが正解した６２点というスコアから、
５点の問題、８点の問題が最低いくつ存在するのかを計算したあとに、テストが全部で何問あるのかを考えたほうがいいと思います。

正解はこのブログの最後に載せておきます。

こういった問題が35問入っています。

毎日1ページやると、大体1ヶ月ちょっとで終わります。

思考力ひろがるワークとは違って、５つの思考回路を総合的に向上させるため、回路別に章分けされております。

まとめ

この「ちょっとむずかしめ編」においては、小学校低学年では難しいところがあると思います。少なくとも５～６年生以上が対象だと思います。

ところどころに、算数の公式を理解していないと解けないものもありましたので、そういった問題は親子で一緒になって解いて頂ければと思います。

教材自体も『5分で～』とタイトルに付いているだけあって、5分考えて分からなかったらヒントを見て良いことになっています。
うちの場合は、ヒントを見てちょっとしても分からなかったら答えを見て良いことにしています。

そのため、そこまで時間をかけずに出来るので、そこは良いポイントなのかなぁと思っています。

手軽にできるので、みなさんも是非購入し、親子一緒になって問題に挑戦してみてください！
※私はズボラなので３冊一気に購入してしまいましたが、結構増版している良いテキストなので、どうせやるだろうと全部買ってしまうのも一つの手かなぁと思います。

正解：８の段で一桁目が２になるのは、８×４＝３２だけなので、
６２点　＝　８点×４問　＋　５点×６問
８点の問題が少なくとも４問あることが分かりました。
５点の問題＝５の段ということで、５の段では簡単に一桁目が０になるようにできます。
それに合わせるように８の段でも一桁目を０にするには、
８点×５問＝４０点がありますね。残りの６０点は５点の問題の数となるので、
５点×１２問＝６０点となります。
よって答えは、５点が１２問、８点が５問となります。